
D'où la fonction en Java qui convertit un nombre entier en base dix en un nombre en base deux sur 32 bits.
static int[] decToBin(long nombre){
int[] rule = new int[32];
long quotient = nombre;
int indice = 0;
int reste;
while(quotient > 0){
reste = (int)quotient % 2;
rule[indice] = reste;
quotient = quotient/2;
indice = indice + 1;
}
for(int i = indice;i <= 31;i = i+1){
rule[i] = 0;
}
return rule;
}
Pour représenter un entier relatif en machine sur 2n bits = 32 ou 64 nous allons utiliser la complémentation à 2.
Soit x un entier relatif positif plus petit que 2n-1 -1 = alors son représentant en machine est le nombre en base deux correspondant à x.
Soit x un entier relatif négatif compris entre - 2n-1 et -1 alors son représentant en machine est le nombre en base deux correspondant à x + 2n. D'où la fonction java suivante pour 32 bits:
static int[] relatifToBit(long nombre){
long base = 4294967296l;
long plusGrandPositif = 2147483647l;
if (( nombre >= 0) & (nombre <= plusGrandPositif)){
return decToBin(nombre);
}
else{return decToBin(nombre+base);}
}
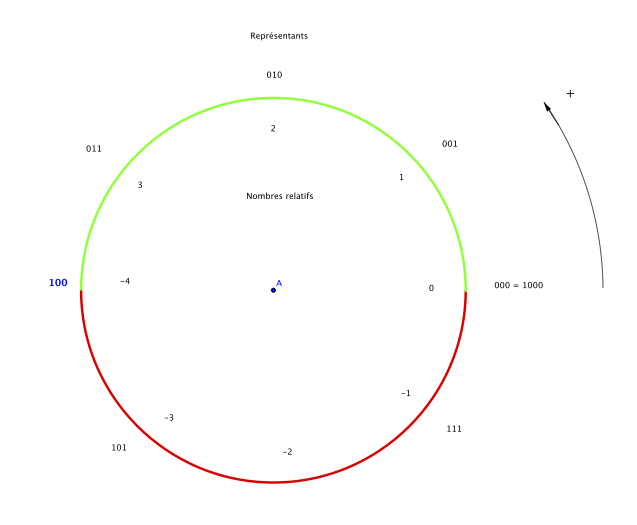
Si on change chaque bit d'un mot m de 2n bits en son contraire on obtient un nouveau mot m' tel que m + m'=11......1 (les n bits sont des 1)
Donc m+(m'+1)=1......0=2n
Donc pour trouver le représentant de x un entier relatif négatif compris entre - 2n-1 et -1 d'abord on cherche le représentant de -x
Puis on change les bits un à un et on ajoute un.
static ....................InverseBit(.........){
int[] mot2 = new int[32];
for(.........){
if(........){
..........
}
}
return ........
}
static ..........ajouteUn(................){
int retenue = ..........;
// tant que la retenue vaut 1 on continue d'ajouter
while(...........................){
if(.......................){
.....................
}
else{
.................
}
}
return ..................;
}
Télécharger ici la classe permettant de le faire (à compléter)
Java propose des fonctions déjà comme celle de la classe Integer: Voir Ici la documentation Java pour la classe Integer
Que fait la fonction suivante de la classe Integer (à ne pas confondre avec le type primitif integer ) ?
public static String toBinaryString(int i)
Returns a string representation of the integer argument as an unsigned integer in base 2.
The unsigned integer value is the argument plus 232 if the argument is negative; otherwise it is equal to the argument. This value is converted to a string of ASCII digits in binary (base 2) with no extra leading 0s .
Voir Ici la documentation Java pour la classe Float
Voir Ici la documentation Java pour la classe Double
Pour représenter les nombres à virgule il y a une norme édité en 1985 la norme IEEE 754
L'entier 4 sur 32 bits est représenté par 0000 0000 0000 0000 0000 0000 0000 0100
Par contre le nombre à virgule 4.0 sur 32 bits (float) est représenté par 0100 0000 1000 0000 0000 0000 0000 0000
Ce n'est pas la même chose donc ne pas mélanger les types
Si en machine il y a un mot de 32 bits s-e-m avec s sur un bit , e sur 8 bits et m sur 23 bits alors le nombre est (-1)s *2e-127*(1,m)2
Si en machine il y a un mot de 64 bits s-e-m avec s sur un bit, e sur 11 bits et m sur 52 bits alors le nombre est (-1)s *2e-1023*(1,m)2
Regardons sur un exemple comment trouver le représentant de 2,1
D'abord 2,1 = 1,05 x 2 donc le représentant de l'exposant est 127+1=128 et le bit de signe est 0
128 en base deux s'écrit sur un octet 1000 0000 donc on a le mot 0 1000 0000 (sans la mantisse)
Il reste à écrire 0,05 en binaire. On multiplie par 2 jusqu'à ce que on dépasse 1. On a multiplié 4 fois par 2 avant de dépasser 1
Donc pour l'instant 0,05 = 00001
A la cinquième multiplication par 2 on obtient 1,6 on met donc un bits à 1 à la cinquième position et on prend la partie fractionnaire et on recommence
0,6 x 2 = 1,2 le sixième bit est à 1 donc pour l'instant 000011
0,2 x 2 = 0,4 puis 0,4 x 2= 0,8 puis 0,8 = 1,6 donc 0000 11001
On prend la partie fractionnaire 0,6 que l'on multiplie par 2 et on obtient 1,2 donc on a le mot 0000 110011 puis il y a répétition
Donc sur 23 bits 0000 1100 1100 1100 1100 110
La représentation de 2,1 en machine sur 32 bits est 0 1000 0000 0000 1100 1100 1100 1100 110
Si on utilise la méthode Java toBinaryString pour afficher le représentant de 2,1 on aura:
1000 0000 0000 1100 1100 1100 1100 110 , le bit de signe étant nul n'est pas affiché .
Exécuter le programme et le modifier pour expliquer ce qui se passe.
class ErreurArrondi{
public static void main (String args[]){
double x, y;
x = 1.0;
y = x +1.0;
while (y-x == 1.0){
x = x*2.0;
y = x + 1.0;
}
}
}
Exécuter et modifier le programme pour comprendre ce qui se passe
class ErreurArrondi2{
public static void main (String args[]){
double a;
int n;
a = 0.0;
for (n = 1;n <= 10;n = n+1){
a = a+0.1;
System.out.println(a);
}
}
}