Il s'agit dans un premier temps de mettre au point une tortue Logo en Java.
Logo est un langage pédagogique comme Scratch pour aprendre à programmer aux plus jeunes. Comme Scratch c'est un langage essentiellement graphique.
La tortue Logo est un objet à 3 attributs :
Il sera représenté ici sous la forme d'un tableau d'entiers int de taille 3.
Les fonctions associées à cet objet sont:
Télécharger ici la classe Dessin
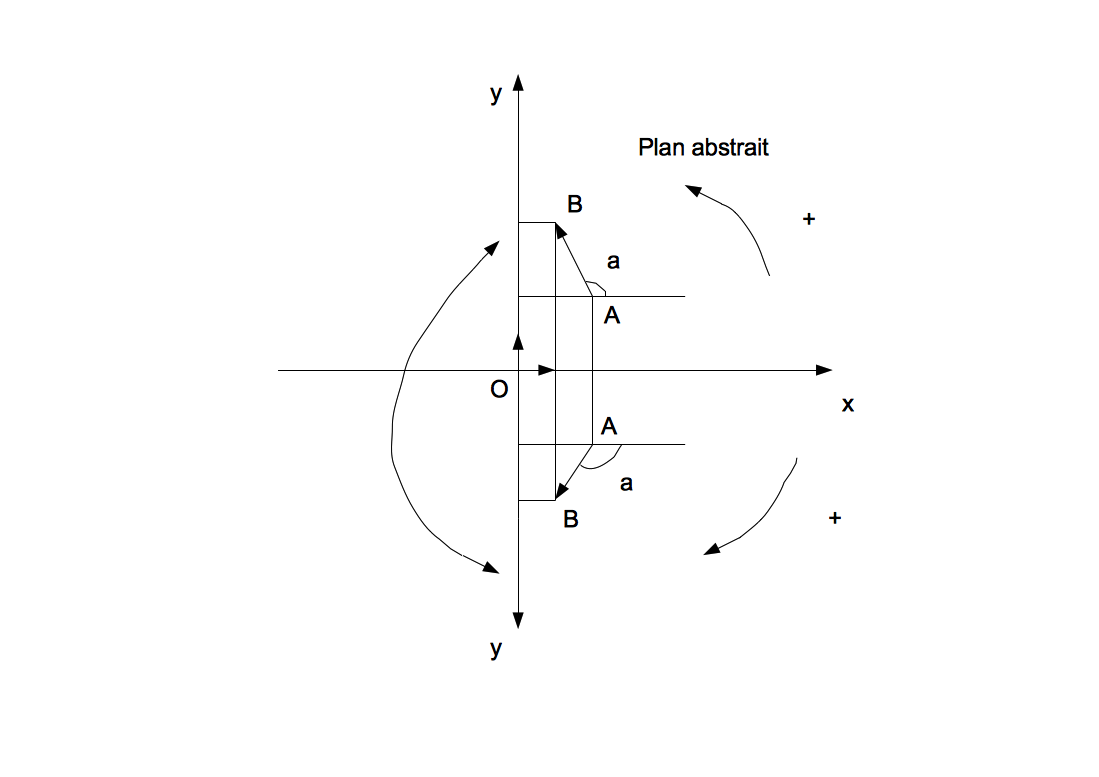
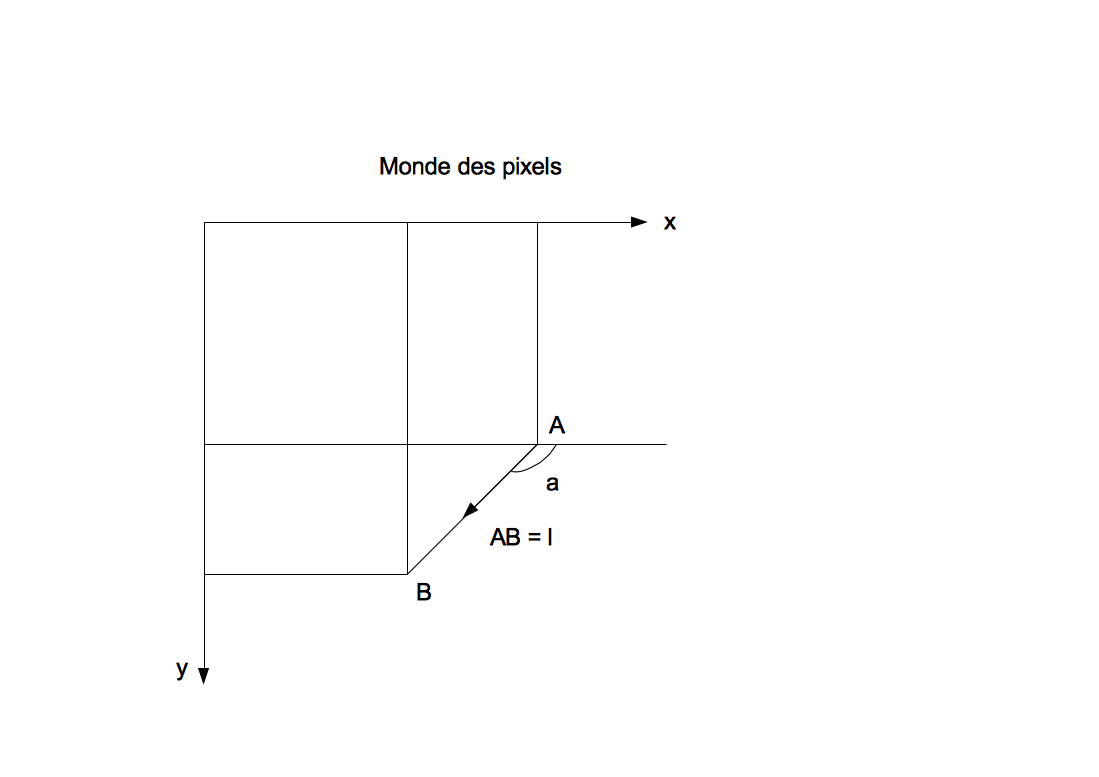
Mettre au point la fonction avancer, en la testant sur quelques cas particuliers.(Aide: voir schémas ci-dessous)

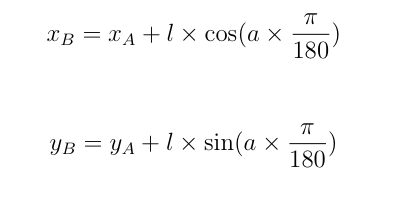
La courbe de Koch est l'une des premières courbes auto-similaires
Elle a été inventée en 1906 par le mathématicien suédois Helge von Koch (1870 - 1924).
Elle peut-être décrite récursivement ainsi:
Lorsque la tortue doit tracer un segment de longueur l partant de A , elle délègue à 4 autres tortues le soin de tracer des segments de longueur trois fois moins long et dans des directions représentées sur le schéma suivant (CDE est un triangle équilatéral), et ceci sauf si la longueur l est inférieure à une valeur critique fixée au préalable (par exemple 3 pixels) dans ce cas elle avance de la longueur l
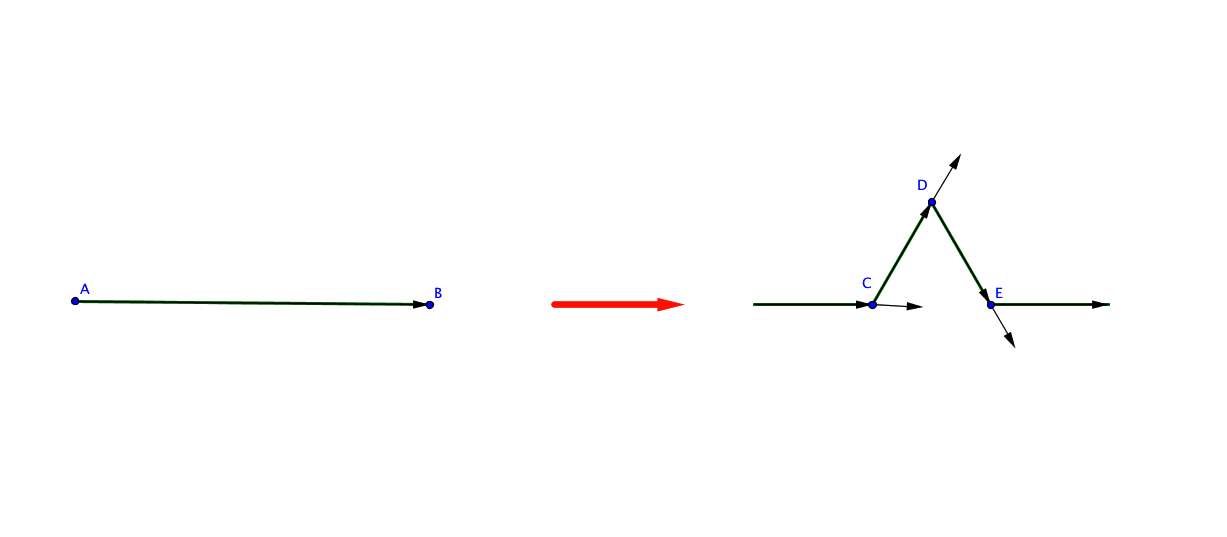
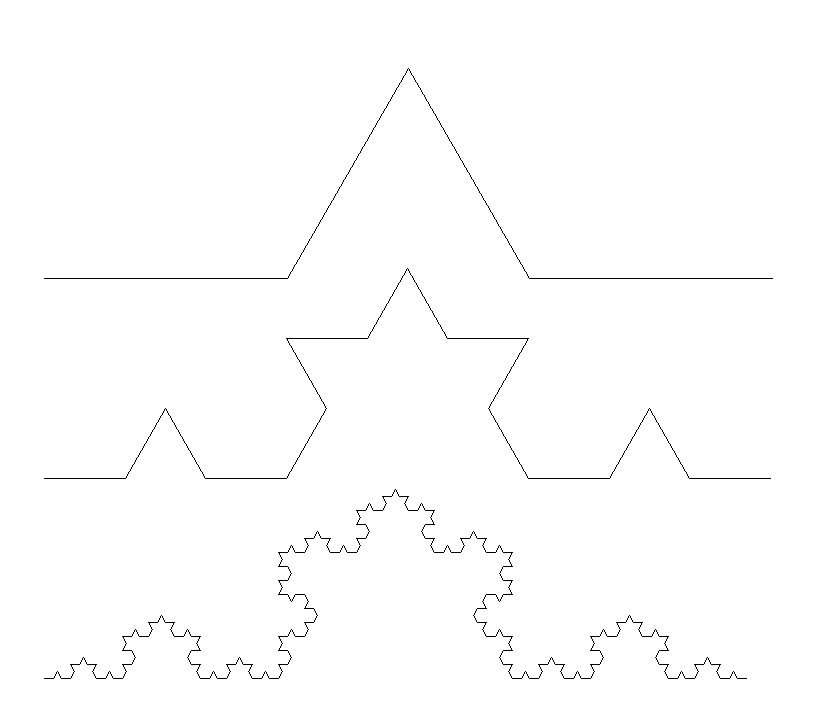

A l'usage on se rend compte que nos fonctions ne sont pas assez précises
Nous avons utilisé la fonction koch(729) à côté d'une droite test de longueur 729 = 36
On observe une perte de précision lorsque la complexité de la courbe augmente
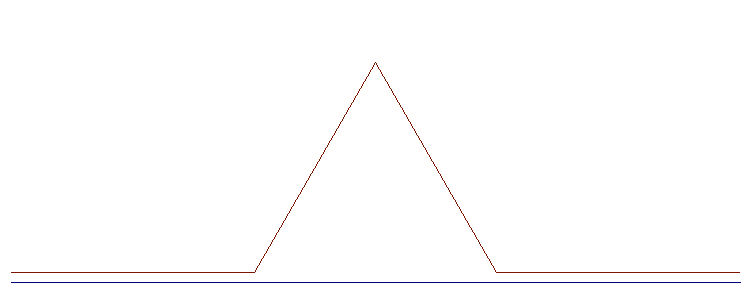
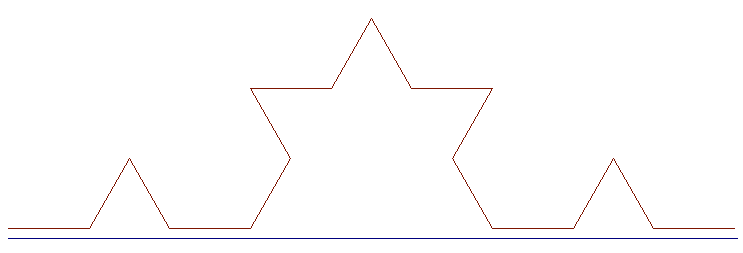
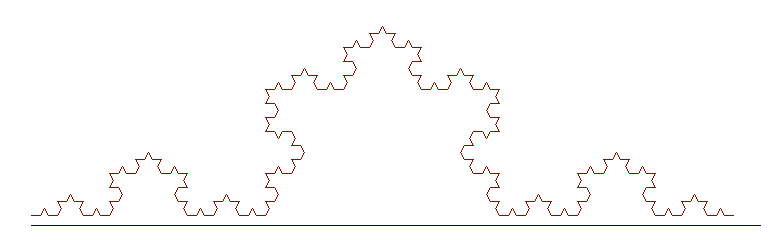
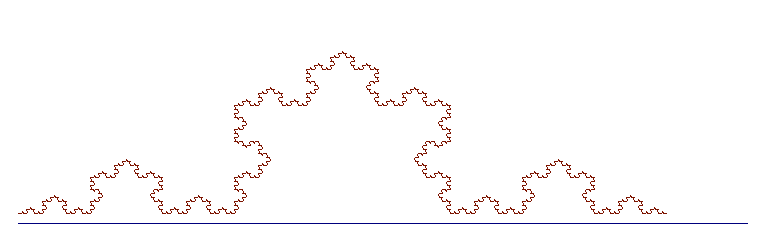
Pour atténuer ces problèmes il semble préférable d'utiliser la fonction Isn.drawLine avec des points ayant des coordonnées double au lieu de int, laissant à Java arrondir au mieux et de placer ensuite les points.
On modifie la tortue:
La fonction avancer devient une traduction littérale des formules mathématiques (c'est plus simple)
static void avancer(int l){
double x_old = tortue[0];
double y_old = tortue[1];
double a = tortue[2];
tortue[0] = tortue[0]+ Math.cos(a)*l;
tortue[1] = tortue[1]+ Math.sin(a)*l;
Isn.drawLine(x_old,y_old,tortue[0],tortue[1],0,0,0);
}
C'est mieux lorsque la longueur est une puissance de 3 . Ci-dessous on a tracé la courbe pour l = 729 puis pour l = 243 = 35
mais il y a encore une perte de précision pour l = 300 et l = 400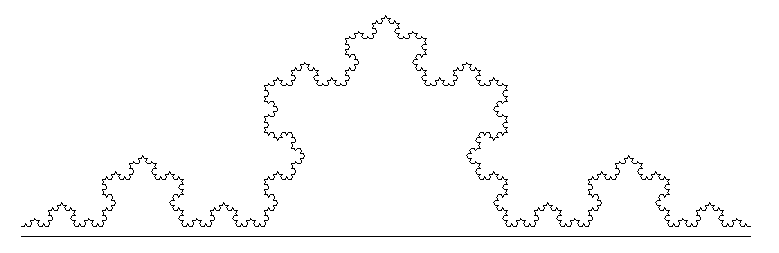
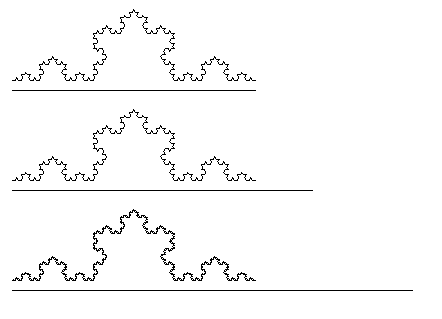
En faisant en sorte que la longueur l soit de type double dans la fonction avancer et la fonction koch il n'y a plus de problème de précision
Voir ci-dessous l = 300 et l = 400
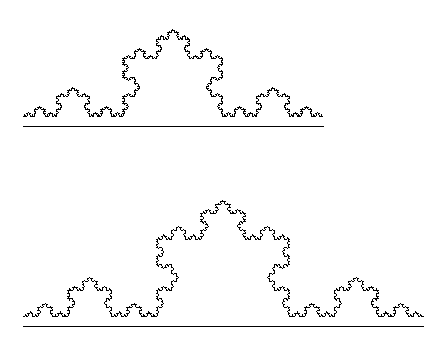
On garde la même idée , c'est à dire la tortue avance et trace un segment si la longueur est en dessous d'une valeur critique mais on change de règle par exemple celle-ci illustrée graphiquement ci-dessous

On obtient alors ce genre de courbe:
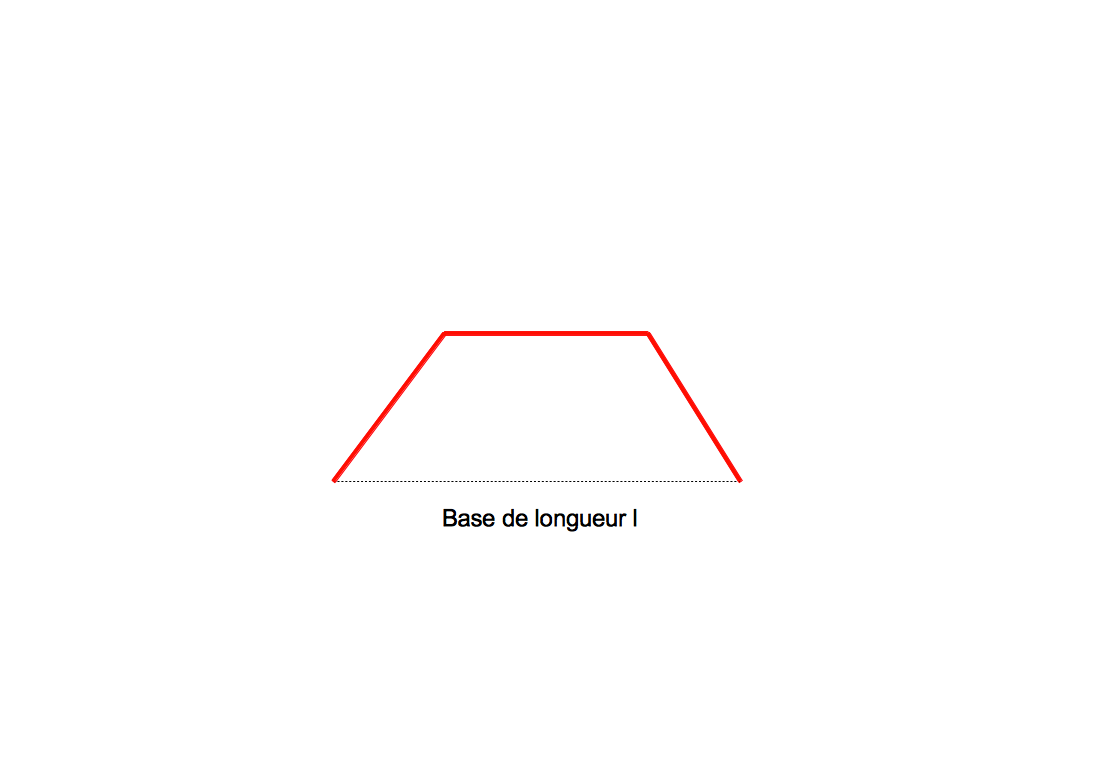
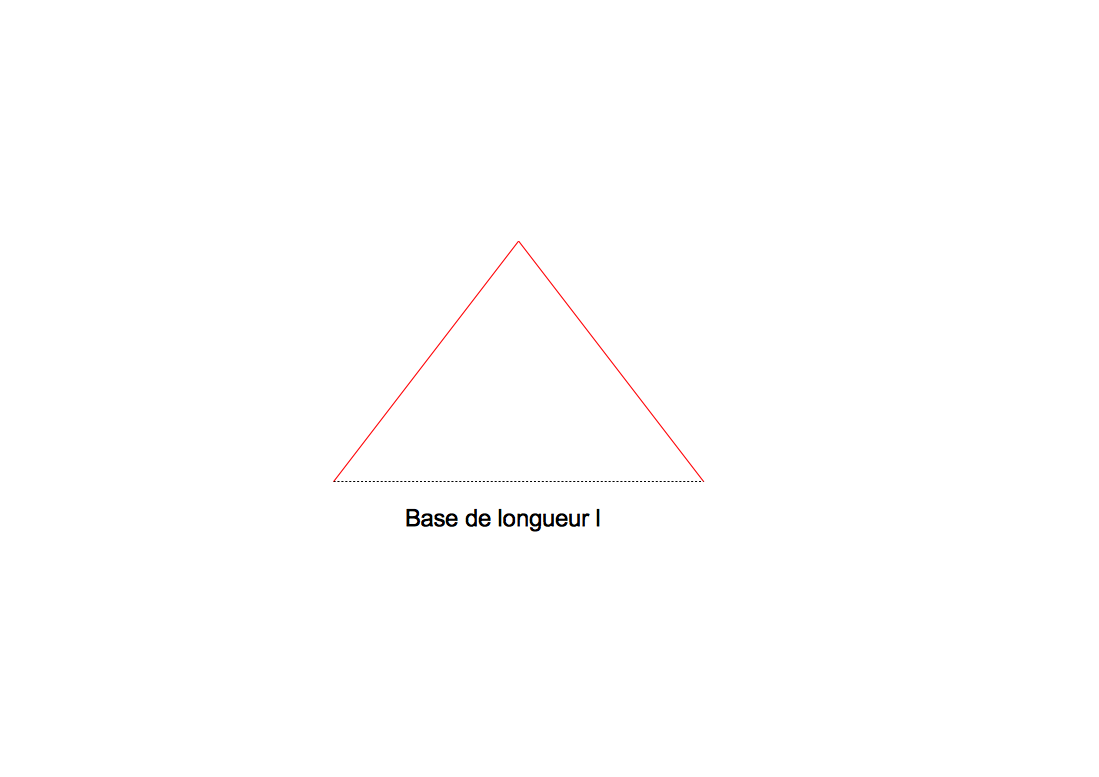
Si la longueur est en dessous d'une valeur critique la tortue n'avance pas de l et ne trace donc pas un segment de longueur l mais trace une ligne polygonale régulière dont la base a pour longueur l
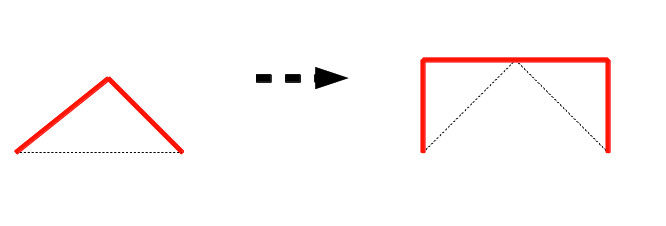
Il faut donc mettre au point au préalable une fonction qui fait tracer à la tortue une ligne polygonale comme un "accent circonflexe" la moitié du contour d'un carré.
Puis définir une règle comme celle -ci:
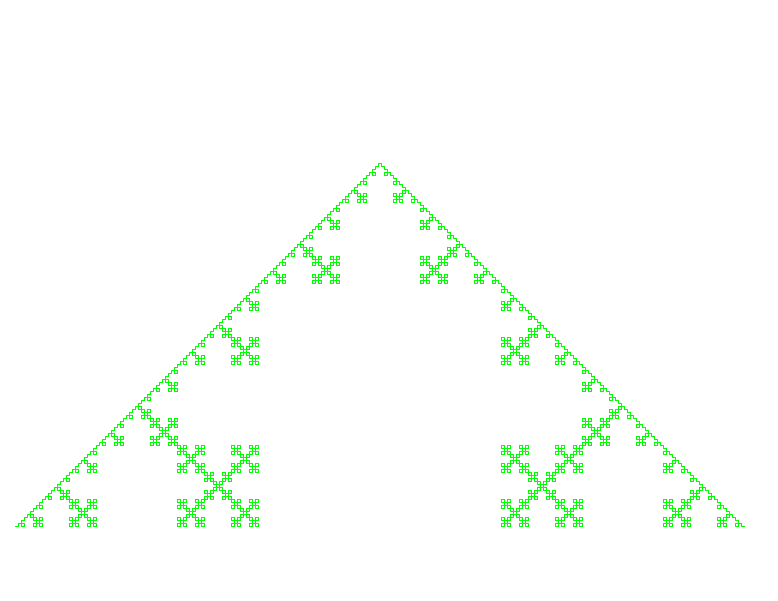
On obtient alors la courbe du crabe:

On définit souvent une règle de non-chevauchement :(voir ci-dessous) l'arc est une fois tracé d'un côté de la base, une fois de l'autre
On obtient alors la courbe du Dragon:
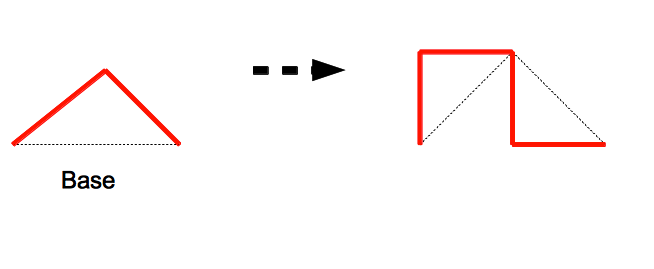

Cette fois-ci en dessous de la valeur critique la tortue trace une sorte de pont , contour de trois triangles équilatéraux imbriqués et de côté l/2:
La courbe obtenue est le triangle de Sierpinski